Proposte didattiche a base di origami

Incontri sulla didattica con l'origami sulla piattaforma Zoom a cura del Centro Diffusione Origami.
L'iniziativa si rivolge espressamente a insegnanti ed educatori e si prefigge di organizzare un appuntamento periodico nel quale piegare ed analizzare un dato modello origami per inquadrarlo nell'ambito della didattica scolastica. In questo modo intendiamo offrire ai partecipanti alcuni spunti concreti da usare nel proprio contesto educativo: ogni insegnante potrà riproporre i vari percorsi ai propri studenti con i necessari adattamenti, in base al livello scolare d'interesse. Gli incontri si svolgono esclusivamente in lingua italiana.
Informazioni e contatti: info@origami-cdo.it
Comitato organizzativo: Stefania Serre (stefyserre@gmail.com), Francesco Decio (fradecio3@gmail.com), Antonio Coiana (host).

OriDidaZoom n. 25 - Le basi dell'origami
23 aprile 2025 Durata: circa 90'
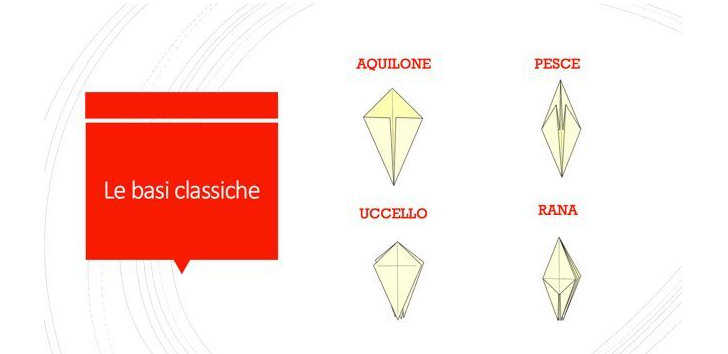
Le basi dell'origami
Un laboratorio per scoprire le quattro basi fondamentali dell’origami: aquilone, pesce, uccello e rana.
Indirizzeremo la nostra attenzione sui crease pattern e le ricorrenze dei triangoli e alette nelle varie basi.
Concluderemo piegando un modello semplice di Robert Lang.
Con Marco Torredimare.
Materiale necessario:
- Fogli kami 15x15


OriDidaZoom n. 24 - Natalizio
11 dicembre 2024 Durata: circa 90'

OriDidaZoom Natalizio
Natale è ormai alle porte e ovunque si vedono i vari simboli che lo annunciano. Tra i tanti, alcuni sono classici: l'albero, la stella e Babbo Natale. Proporremo quindi una versione di ciascuno dei tre, pieghe semplici, anche semplicissime, ma sempre con un occhio alla geometria nascosta tra le pieghe. E le sorprese non mancheranno.
Con Francesco Decio e Stefania Serre.
Materiale necessario:
- Per piegare l'albero servono 5 fogli quadrati bicolore marrone/verde oppure marrone/ bianco o anche bianco/verde, preferibilmente con lato 7,5 cm o poco più.
- Per piegare la stella servono 5 fogli quadrati. A seconda delle proprie preferenze è possibile scegliere quadrati con lato 15 cm. oppure da 11,8 cm. o ancora da 7,5 cm. E' da preferire la scelta di 5 colori diversi ma in ogni caso i fogli possono essere bicolore o monocolore.
- Per piegare Babbo Natale serve un foglio quadrato bicolore bianco / rosso preferibilmente con lato da 10 cm al massimo.
Scarica i diagrammi :
- Alberello natalizio [pdf] di Francesco Decio
- Stellina tascabile [pdf] di Francesco Decio


OriDidaZoom n. 23 - Tutti per... 8
novembre 2024 Durata: circa 90'

Tutti per... 8
In quanti modi si può ricavare con le pieghe un ottagono regolare da un quadrato? E con l'ottagono ottenuto cosa si può piegare poi? Quali considerazioni possiamo fare sulle pieghe che si vengono a creare?
Risponderemo a queste e altre domande nel prossimo OriDidaZoom. Con Francesco Mancini.
Materiale necessario:
- Fogli A4
- fogli quadrati
- un taglierino


OriDidaZoom n. 22 EXTRA - Un altro cubo a metà!
maggio 2024 Durata: circa 90'

Un altro cubo a metà!
Materiale necessario:
- 9 fogli quadrati, anche monocolore da 80 g/m² (carta da fotocopie) da 210 mm di lato in 3 colori diversi (ad esempio 3 rossi, 3 verdi e 3 gialli)
- 6 fogli quadrati, anche monocolore da 80 g/m² (carta da fotocopie) da 210 mm di lato di colore bianco o comunque di un colore diverso dai precedenti
- un taglierino CDO o un cutter


OriDidaZoom n. 22 - Cubi dimezzati?
15 maggio 2024 ore 21.00, mercoledì Durata: circa 90'

Cubi dimezzati?
Tra le sezioni piane di un cubo ce ne sono alcune davvero speciali: quelle che hanno la proprietà di dividere il cubo esattamente a metà. Quali sono? E quante? Vi proponiamo di realizzarne insieme due, molto diverse tra di loro, che ci sapranno guidare attraverso molteplici e interessarti osservazioni sulla geometria piana e dello spazio.
Materiale necessario:
- 9 fogli quadrati, anche monocolore da 80 g/m² (carta da fotocopie) da 210 mm di lato in 3 colori diversi (ad esempio 3 rossi, 3 verdi e 3 gialli)
- 6 fogli quadrati, anche monocolore da 80 g/m² (carta da fotocopie) da 210 mm di lato di colore bianco o comunque di un colore diverso dai precedenti
- un taglierino CDO o un cutter
Scarica i diagrammi :
- 1/2 di cubo [pdf] di Francesco Decio
- Un mezzo di cubo [pdf] di Francesco Decio

OriDidaZoom n. 21 - CROSS puzzle: un tangram alternativo
23 aprile 2024 ore 21.00, martedì Durata: circa 90'

CROSS puzzle: un tangram alternativo
In questo incontro proponiamo la realizzazione di un puzzle che ha fatto la sua prima comparsa nol 1899. L'autore è sconosciuto, ma è evidente che si sia ispirato al famoso e classico tangram di provenienza cinese, elaborando un nuovo set di 7 pezzi, comprendente quattro trapezi rettangoli,un pentagono irregolare e due triangoli isosceli. Le composizioni che abbiamo individuato non sono così numerose come per il tangram, che d'altra parte è stato esplorato per secoli, ma con la vostra collaborazione e fantasia, di sicuro ne collezioneremo tante e nuove; non mancheranno i tradizionali ragionamenti su frazioni e rapporti di similitudine che gli studenti esperdi di trangram, potranno mettere alla prova su nuove figure. Si potranno esplorare isometrie e similitudini, trasformazioni dirette e inverse. E la composizione a perimetro minimo? Potrà essere un quadrato?
Materiale necessario:
- 4 fogli formato A6
- 3 fogli formato A5
- 1 foglio formato A4 per il contenitore
- 3 o anche più fogli formato A8 per un uso "extra".
Non è necessario usare fogli colorati. Tuttavia chi volesse usare i colori deve munirsi di almeno 5 colori diversi:
- un colore per 2 fogli formato A6
- un secondo colore per altri due fogli formato A6
- altri tre colori diversi per i fogli formato A5.
- A scelta un sesto colore per il contenitore.
Scarica i diagrammi del Cross Puzzle e del contenitore :
- Cross Puzzle [pdf] di Francesco Decio
Scarica le soluzioni delle figure:
- Cross Puzzle - I 18 poligoni convessi con soluzioni [pdf] (a cura di Luciana Piras, e il contributo di Gisella Maculan e Stefania Serre)
- Cross Puzzle - Soluzioni [pdf]
Scarica le slides di presentazione:
- Presentazione Cross Puzzle di Stefania Serre [pdf]

OriDidaZoom n. 20 - Tassellazioni periodiche e aperiodiche
23 novembre 2023 ore 21.00, giovedì Durata: circa 90'

Tassellazioni periodiche e aperiodiche
Ogni pavimento è una tassellazione del piano. Tuttavia non tutte le figure geometriche sono in grado di tassellare il piano. E non tutte lo fanno allo stesso modo. Vedremo come si sviluppa una tassellazione periodica, ma sperimenteremo più approfonditamente i due famosi tasselli "dardo ed aquilone", di Roger Penrose che danno luogo ad una tassellazione aperiodica, senza trascurare il nuovissimo tassello di Smith: il "cappello" noto anche come "Einstein".
Materiale necessario:
Preparare 4 rettangoli di carta da 80 gr. m² (da fogli da fotocopia) con i lati di 144,5 x 105 mm. I rettangoli in questione non sono reperibili in commercio per cui possiamo immaginare qualche difficoltà a prepararli. In alternativa è possibile usare fogli formato A6 che si ottengono seguendo le istruzioni allegate. I tasselli ottenuti con questo secondo formato avranno una geometria meno precisa per i nostri scopi e di conseguenza la tassellazione sarà meno equilibrata.
Scarica i files:
- Preparazione dei rettangoli [pdf] di Francesco Decio
Scarica i diagrammi:
Deltoide a 72° formato con taglio [pdf] di Francesco Decio
Scarica la presentazione di Stefania Serre [pdf]


OriDidaZoom n. 19 - Forme diverse / volumi equivalenti
30 novembre 2023 ore 21.00, giovedì Durata: circa 90'

Forme diverse / volumi equivalenti
Il laboratorio propone la costruzione, con la tecnica origami, di un tetraedro regolare e di un particolare tetraedro irregolare. Tali tetraedri risulteranno fra loro equivalenti in base al principio dii Cavalieri. In seconda battuta verrà dimostrata l'equivalenza di volume tra 4 tetraedri regolari ed un ottaedro con facce congruenti a quelle dei tetraedri. Andremo ad esplorare la geometria 3D da un punto di vista insolito, ma molto concreto.
Materiale necessario:
- - Un taglierino (cutter)
- - 3 fogli formato A4 preferibilmente in tre colori diversi
- - 2 fogli quadrati di lato 140x140 mm preferibilmente in due colori diversi.
Scarica i diagrammi:
Tetraedri [pdf] di Francesco Decio
Scarica la presentazione di Stefania Serre [pdf]


OriDidaZoom n. 18 - Pieghiamo il dodecaedro e l'icosaedro regolari
16 novembre 2023 ore 21.00, giovedì Durata: circa 90'

Pieghiamo il dodecaedro e l'icosaedro regolari
Il triangolo equilatero è piuttosto ben conosciuto nella scuola. Al contrario il pentagono è relativamente poco "frequentato". Entrambi però hanno un posto di rilievo nella geometria solida ed in particolare tra i solidi platonici: permettono infatti di costruire i due solidi regolarii duali con massimo numero di facce (e vertici). Nel laboratorio proponiamo la realizzazione, con la tecnica dell'origami modulare, del dodecaedro regolare a facce pentagonali (con ottima approssimazione geometrica) e dell'icosaedro regolare.
Dai laboratori proposti da Stefania Serre e Francesco Decio al 37° Convegno "Incontri con la Matematica" tenuto a Castel an S.Pietro Terme l'11 novembre 2023.
Materiale necessario per il DODECAEDRO regolare:
12 (dodici) fogli rettangolari da 80 gr/m² (da fotocopia) i cui lati misurino 148.5 mm x 204.6 mm.
Immaginiamo che per molti partecipanti sarà un problema reperire fogli con queste misure poichè non sono in commercio.
In alternativa è possibile usare 12 (dodici) fogli rettangolari da 80 gr/m² (da fotocopia) i cui lati misurino 148.5 mm x 210 mm (foglio A5).
In questo secondo caso sarà possibile ottenere comunque il solido in questione anche se con una geometria meno precisa.
Materiale necessario per l'ICOSAEDRO regolare:
70 (settanta) foglietti rettangolari da 80 gr/m² con i lati da 105 mm x 60.6 mm.
Anche tali foglietti non sono in commercio, per cui è necessario provvedere personalmente a ritagliarli da vari fogli A4 (da fotocopia).
Trovate le istruzioni per ritagliare i foglietti con le misure esatte da fogli formato A4.
In alternativa ci si può rivolgere a ditte specializzate (tipografie, centri stampa ecc. ecc).
Ci permettiamo di ricordare che è fondamentare rispettare le misure indicate (105 x 60.6 mm).
Diversamente sarà difficile ottenere una figura equilibrata.
Consigliamo di preparare 20 foglietti di un colore, altri 20 di un colore diverso ed infine gli altri 30 di un terzo colore.
Scarica i files:
- Preparazione dei fogli per il dodecaedro [pdf] di Francesco Decio
- Preparazione fogli 1 x radice di 3 [pdf] di Francesco Decio
Scarica i diagrammi:
- Dodecaedro [pdf] di Francesco Decio
- Icosaedro a tessere triangolari [pdf] di Francesco Decio


OriDidaZoom n. 17 - 4 3 2 1 ... si ricomincia!
7 settembre 2023 ore 21.00, giovedì Durata: circa 90'

4,3,2,1... si ricomincia!
Settembre mese di ripartenze: ricomincia la scuola e ricomincia anche OriDidaZoom, perché la voglia di piegare insieme con uno sguardo alla didattica non ci ha certo lasciati durante questi mesi. Francesco Decio e Stefania Serre vi propongono 4 tessere da coniugare con applicazioni aritmetiche, geometriche e artistiche. Qualcuno ha già sperimentato, producendo composizioni meravigliose che non possiamo fare a meno di condividere!
Foto e composizioni di Barbara Sbrega. Modelli di Francesco Decio.
Cosa occorre
- Ogni tessera si ricava da sottomultipli di kami 15 x 15. Preparate quindi dei fogli 15 x 15 da tagliare per realizzare tanti piccoli moduli!
Scarica i diagrammi:
- Parallelogram [pdf] di Francesco Decio
- Da 4 quarti a 1 quarto [pdf] di Francesco Decio
Scarica la presentazione di Stefania Serre [pdf]


OriDidaZoom n. 16 - Pieghe in gioco
10 novembre 2022 ore 21.00, giovedì Durata: circa 90'

Pieghe in gioco
Imparare giocando è una specie di sogno comune a studenti ed educatori. Dietro allo stupore ed innegabile divertimento derivante dalla piegatura di alcuni modelli origami dalle pieghe molto semplici, è possibile esaminare della bella geometria in modo tanto rigoroso quanto tangibile, pratico e concreto. Piegare per credere!
Con Stefania Serre e Francesco Decio
Cosa occorre
- Un foglio quadrato da 7 x 7 cm. di carta monocolore da 80 gr/m² ( da foglio A4)preferibilmente di colore verde.
- Un foglio formato A4 preferibilmente bianco da 80 gr/m².
- 2 fogli da 14 x 14 cm di carta monocolore da 80 gr/m² preferibilmente di colore diverso tra loro.
- 4 o anche più fogli da 14 x 14 cm di carta monocolore da 80 gr/m² colori a piacere.
Scarica i diagrammi:
- Cavalletta [pdf]
- Quasar [pdf]
- Ribaltino [pdf]
Scarica la presentazione di Stefania Serre [pdf]


OriDidaZoom n. 15 - Pitagora
10 novembre 2022 ore 21.00, giovedì Durata: circa 90'

Pitagora
Il teorema di Pitagora è un classico della geometria oltre che un caposaldo, pietra miliare e passaggio obbligato nella didattica.
Sono centinaia le dimostrazioni in circolazione fin dai tempi e luoghi più antichi.
Tra le tante proponiamo una versione origami tratta da un'idea geniale del grande Sam Loyd per un particolare triangolo rettangolo.
La versione permette di osservare, calcolare e controllare visivamente la tesi del teorema stesso.
Piegare per credere!
Con Stefania Serre e Francesco Decio
Cosa occorre
- 1 rettangolo di carta monocolore da 80 gr/m² da 10,5 x 21 cm (metà quadrato ottenuto da foglio A4) di colore azzurro.
- 2 rettangoli di carta monocolore da 80 gr/m² da 10,5 x 21 cm (metà quadrato ottenuto da foglio A4) di colore rosso.
- 2 rettangoli di carta monocolore da 80 gr/m² da 10,5 x 21 cm (metà quadrato ottenuto da foglio A4) di colore verde.
- Altri 4 rettangoli di carta monocolore da 80 gr/m² da 10,5 x 21 cm (metà quadrato ottenuto da foglio A4) di colore giallo.


OriDidaZoom n. 14 - Costruzioni ottagonali
3 novembre 2022 ore 21.00, giovedì Durata: circa 90'

Costruzioni ottagonali
Composizioni e scomposizioni di ottagoni singoli e multipli in cerca di relazioni proprietà e regolarità.
Con Barbara Sbrega e Luciana Piras
Cosa occorre
- fogli 15x15 (non servono bicolori) possibilmente di 3 colori diversi, fogli A4 (o comunque della serie A)
Scarica la presentazione [pdf]


OriDidaZoom n. 13 - Tessera triangolare rompicapo
13 ottobre 2022 ore 21.00, giovedì Durata: circa 90'

Tessera triangolare rompicapo
Una tessera piuttosto versatile che permette varie composizioni... con sorpresa!
Con David Medina (Perù), traduzione di Stella Ricotti (Argentina)
Cosa occorre
- almeno 14 fogli di kami bianca/colore da 7,5 x 7, 5 cm
Scarica i diagrammi della tessera triangolare [pdf]


OriDidaZoom n. 12 - Triangoli Rep-Tiles
1 giugno 2022 ore 21.00, mercoledì Durata: circa 90'

Triangoli Rep-Tiles
Triangoli rettangoli, irrazionalità, rep-tile, simmetrie, isometrie, frattali, Pitagora, Euclide...In un colpo solo! Piegheremo diverse tessere triangolari per creare figure simili più grandi con pattern particolari.
Con Luciana Piras e Barbara Sbrega
Cosa occorre
- Carta kami bicolore (è importante) in formato 15x15 cm. Un taglierino o cutter, perché lavoreremo con un formato di carta 2/rad3
Scarica la presentazione [pdf]


OriDidaZoom n. 11 - Diamoci un taglio! La matematica con un colpo di forbici
4 maggio 2022 ore 21.00, mercoledì Durata: circa 90'
Diamoci un taglio! La matematica con un colpo di forbici
Cosa succede se deviamo un po' dalla regola che nell'origami non si possono usare le forbici e dopo una serie di pieghe facciamo un unico passante?
Inaspettatamente le forme possibili sono molteplici e, tra poligoni, stelle, simmetrie, riservano sorprese a ogni colpo di forbici.
Con Francesco Mancini
Cosa occorre
- Carta kami e forbici
Scarica la presentazione di Francesco Mancini [pdf]
Siti e documenti di riferimento:


OriDidaZoom n. 10 - sTRAPieghiAmo
31 marzo 2022 ore 21.00, giovedì Durata: circa 90'

sTRAPieghiAmo
Con Gabriella Romano piegheremo alcuni puzzle con protagonista il trapezio, poligono che spesso appare "anonimo" o comunque meno frequentato di altri quadrilateri, seppur ricco di proprietà.
Da solo o combinato ad altri poligoni può offrire spunti di riflessione senza rinunciare al divertimento.
Modelli di Francis Ow.
Cosa occorre
- Carta kami o carta da fotocopie


OriDidaZoom n. 9 - Origami 3,14
14 marzo 2022 ore 21.00, lunedì Durata: circa 90'

Origami 3,14
Nella giornata mondiale della matematica non potevamo mancare all'appuntamento con OriDidaZoom! Non vi promettiamo la quadratura del cerchio ma nel pi-day non potevamo esimerci dal soffermarci sui rapporti tra pieghe e cerchi.
Cosa occorre
- Una buona scorta di fogli tagliati a cerchio. Ci sono compassi che tagliano la carta, oppure si può disegnare un cerchio usando la classica scodella o un piatto e poi ritagliarlo. Oppure ancora appoggiare un CD ed incidere direttamente la carta con un cutter. Naturalmente i fogli a cerchio si trovano anche in commercio, ad esempio quelli utilizzati per gli hamburger.
Scarica i diagrammi: Cubetto con strisce 1 x 4 - Di Francesco Decio [pdf]


OriDidaZoom n. 8 - Triangoli noti e... divertimenti imprevisti
24 febbraio 2022 ore 21.00, giovedì Durata: circa 90'
Triangoli noti e... divertimenti imprevisti
L'oggetto dell'incontro di OriDidaZoom sarà il poligono più semplice che ci sia: il triangolo. Lo useremo come strumento per esplorare alcuni concetti matematici fondamentali come le dissezioni e le similitudini, ma lo renderemo anche protagonista di un trucchetto curioso.
Cosa occorre
- 5 quadrati da 15 x 15 cm di classica Kami bianca su un lato.
- 4 fogli formato A4 di cui 3 in colore diverso.
- Un taglierino o cutter.
Una procedura simile è stata presentata da Francesco Decio anche al Convegno CDO 2021, proponendo anche un piccolo rompicapo: se te lo sei perso puoi rivedere subito la registrazione di quell'incontro: https://www.youtube.com/watch?v=dDJogLGSxik
Scarica la presentazione di Stefania Serre [pdf]
Scarica i diagrammi:
> Tancrata scomposto - Di Gigi Verri e Francesco Decio [pdf]
> Triangolo isoscele 30 75 75 di Francesco Decio [pdf]


OriDidaZoom n. 7 - Una primavera di rombi
20 gennaio 2022 ore 21.00, giovedì Durata: circa 90'
Una primavera di rombi
Partendo dall'osservazione di un rosone piegheremo insieme alcuni rombi isoperimetrici, realizzando poligoni regolari con interessanti scomposizioni. Esploreremo le loro caratteristiche: angoli, lati e aree e le reciproche relazioni scoprendo altre affascinanti corrispondenze.
Modelli
di Barbara Sbrega e Luciana Piras .
Cosa occorre
Per il formato della carta, fogli quadrati (li useremo bicolore ma monocolore va bene lo stesso) 15x15 cm di colori vari, che verranno tagliati in 4 (quindi 7.5x7.5). Per un tipo di rombo è utile avere della carta in formato 11.8x11.8 ma non è strettamente necessario perché mostreremo come ridurre i fogli 15x15.
> Scarica la presentazione [pdf]


OriDidaZoom n. 6 - Tessere: Festa in testa. Arte e Geometria in origami
20 dicembre 2021 ore 21.00, lunedì Durata: circa 90'
Le Tessere di Rosa
L'incontro, condotto da Rosa Laddago, si intitola: "Tessere: Festa in testa. Arte e Geometria in origami" e vedrà l'esplorazione dell'utilizzo di semplici tessere create da Rosa che consentono la tassellazione del piano con interessanti risultati sia dal punto di vista della composizione artistica che sullo studio di rapporti e proprietà geometriche come la simmetria, la riflessione, la traslazione e altri concetti utili per qualunque livello educativo.
Modelli
Tessere di Rosa Laddago e varianti.
Cosa occorre
Come materiali consigliamo di tenere a portata di mano un buon numero di fogli (almeno 24) in almeno tre colori di classica carta kami da 15 x 15 cm. Il formato ideale per ottenere le tesserine è partire da un quadrato 7,5x7,5 cm ma per prendere confidenza con il modulo andranno bene anche i classici fogli 15x15 cm.
> Scarica la presentazione [pdf]
Scarica i diagrammi delle tesserine di Rosa Laddago (disegni di Francesco Decio):
> Diagrammi della tessera base [pdf]
> Diagrammi delle variazioni [pdf]


OriDidaZoom n. 5 - Il Flexicubo!
21 ottobre 2021 ore 21.00, mercoledì Durata: circa 90'
Flexicubo
...ancora il cubo? Bè, questa volta lo vediamo sotto un aspetto speciale... un cubo magico! Il Flexicubo è un origami di di movimento che sfrutta le tre dimensioni spaziali: x, y e z, un gioco che da tempo ha grande ebbe successo!
Ogni cubetto è formato da tre strisce da 1 x 4 disposte secondo le tre dimensioni. Per montare un cubetto ci vuole meno di un minuto. Per orientarsi tra le tre dimensioni e nella specularità di montaggio richiesta... ci vuole un pò di più. Noi contiamo quantomeno di suscitare qualche riflessione riguardo alla specularità che si presenta relativamente semplice riguardo a figure piane. Su figure 3D la cosa cambia ...e anche notevolmente!
A chi è rivolto l'incontro
L'incontro potrà essere di interesse per tutti gli insegnanti di matematica, (ciascuno lo adatterà con i propri studenti a diversi livelli di approfondimento) e per tutti gli origamisti matematicamente curiosi.
Modelli
Moduli per flexicubo di Francesco Decio
Cosa occorre
Procurarsi carta da 200 grammi o anche cartoncino da 220 grammi di 4 colori diversi e un cutter (taglierino).
Scegliere tre colori dai quali ritagliare per ogni colore 8 strisce da 1 x 4. Tali strisce sono relativamente facili da ottenere ritagliando un quadrato ad esempio di 15 x 15 cm di lato e poi dividendolo tramite pieghe in 4 x 4 quadratini. Le pieghe tracciate servono proprio per il modello. Separare poi ogni striscia (o colonna) ritagliandola dal quadrato stesso. Ritagliare poi dall'ultimo colore rimasto altre 4 strisce da 1 x 4 procedendo come sopra e cioè ritagliando un quadrato da dividere in 4 x 4 per separare poi le 4 strisce o colonne. In totale quindi servono 24 strisce da 1 x 4 divise in tre colori (otto strisce per colore) più 4 strisce sempre da 1 x 4 di un quarto colore. Tenere a portata di mano anche un cutter. Il modello proposto funziona con carta spessa anche ruvida, ma spessa. La classica carta kami o comunque carta sottile NON è adatta per questo modello.
> Scarica la presentazione di Stefania Serre [pdf]
> Scarica i Diagrammi del cubetto a strisce di Francesco Decio [pdf]


OriDidaZoom n. 4 - Pieno/Vuoto?
16 giugno 2021 ore 21.00, mercoledì Durata: circa 90'

Pieno/vuoto?: ancora un percorso all'interno del cubo
Stefania: "Francesco la scuola è finita ed è tempo di riorganizzazione e di esami: per l'ultimo OriDidaZoom ci occorre un bel modello origami che dia soddisfazione di per sé ma che sottolinei la magia della geometria della carta piegata!"
Francesco: "Ce l'ho: il cubo di Maekawa! Ho trovato una nuova tecnica per piegare la griglia iniziale e ho lo sfeno che si inserisce perfettamente nelle facce laterali!"
E così, tra le inevitabili risate per l'ennesimo cubo, inizia la progettazione del prossimo incontro.
Vedremo la corrispondenza di volumi tra diversi solidi che, già significativi di per sé, quando combinati tra loro offrono una visione organica e complessiva dei rapporti tra il generale e il particolare.
A chi è rivolto l'incontro
L'incontro potrà essere di interesse per tutti gli insegnanti di matematica, (ciascuno lo adatterà con i propri studenti a diversi livelli di approfondimento) e per tutti gli origamisti matematicamente curiosi.
Modelli
Cubo di Maekawa, con il permesso dell'autore
Cosa occorre
Come materiale servono 4 fogli in formato A4, meglio se in diversi colori.
> Scarica il Digrammi del cubo di Maekawa disegnati da Francesco Decio [pdf]


OriDidaZoom n. 3 - Ritorno al Quadrato
2 giugno 2021 ore 21.00, mercoledì Durata: circa 90'

Ritorno al quadrato
Con Francesco Mancini. Dopo due puntate dedicate al cubo e ai solidi in questo incontro ci concentreremo sul quadrato sia pensato come poligono sia riferito all'elevamento a potenza. Piegando due modelli semplici aiuteremo i nostri studenti a rendere più concreti e a fare pace con alcuni argomenti di geometria e algebra.
A chi è rivolto l'incontro
L'incontro potrà essere di interesse per tutti gli insegnanti di matematica, (ciascuno lo adatterà con i propri studenti a diversi livelli di approfondimento) e per tutti gli origamisti matematicamente curiosi.
Modelli
Kit del piccolo origamista algebrista euclideo di Francesco Mancini
Cosa occorre
1 quadrato ricavato da un A4 e 2 quadrati ricavati da 2 A5. Qualunque tipo, bicolore.
Download
> Scarica la presentazione [pdf]
> Scarica il Kit del piccolo origamista algebrista euclideo di Francesco Mancini[pdf]


OriDidaZoom n. 2 - Cubi con sorpresa
19 maggio 2021 ore 21.00, mercoledì Durata: circa 90'

Cubi con sorpresa
In questo incontro piegheremo alcune tra le figure solide più comuni e le metteremo in relazione tra loro in una prospettiva insolita. Avremo infatti modo di analizzare alcune composizioni e scomposizioni con tetraedro e ottaedro anche in relazione con il cubo, attraversando stelle e stellazioni da 2D a 3D. Procederemo insomma a esplorare il mondo della geometria solida, utilizzando in particolare un modulo semplice ma significativo e molto versatile.
A chi è rivolto l'incontro
L'incontro potrà essere di interesse per tutti gli insegnanti di matematica, (ciascuno lo adatterà con i propri studenti a diversi livelli di approfondimento) e per tutti gli origamisti matematicamente curiosi.
Modelli
Vari
Cosa occorre
Il materiale da piegare si presenta "abbondante": vi chiediamo quindi di procurarvi almeno una dozzina di fogli formato A4 meglio se in 4 colori.
Download
> Scarica la presentazione di Stefania Serre [pdf]
> Scarica i diagrammi tessere TRIANGOLARI e QUADRATE di Francesco Decio [pdf]
> Scarica i diagrammi di Modelli 3D con tessere triangolari di Francesco Decio (tetraedro, ottaedro, stella Octangula, cubo dalla stella Octangula) [pdf]


OriDidaZoom n. 1 - B x h / 3
5 maggio 2021 ore 21.00, mercoledì Durata: circa 90'

B x H / 3
La formula per calcolare il volume della piramide suscita da sempre un po' di incredulità negli studenti: quel 'diviso tre' sorprende e non convince. Ben vengano quindi tutte le prove sperimentali per sostenerne la validità; noi ne proporremo una visiva e concreta, un modello origami di Francesco Decio che, nella sua immediatezza, risulta assolutamente convincente. Nel corso dell'incontro sarà anche proposto un metodo originale (di cui illustreremo anche la dimostrazione algebrica/geometrica/analitica) per ottenere uno o due quadrati dal formato A4.
A chi è rivolto l'incontro
L'incontro potrà essere di interesse per tutti gli insegnanti di matematica, (ciascuno lo adatterà con i propri studenti a diversi livelli di approfondimento) e per tutti gli origamisti matematicamente curiosi.
Modelli
Piramidi rette e contenitore, di Francesco Decio
Cosa occorre
Per piegare quanto verrà proposto servono 7 fogli formato A4 di cui almeno 3 in colori diversi e un taglierino o un cutter.
Download
> Scarica la presentazione di Stefania Serre [pdf]
> Scarica i diagrammi del modello di Francesco Decio [pdf]

 English
English 
